Nätutjämning, Kända punkter

Nätutjämning ›› Nätutjämning, Tester ››

Kända punkter

Nätutjämning | Tester | Kända punkter  

Om vi genomfört en tvångsutjämning (utjämning med kända punkter låsta) och fått flera mätningar utpekade som felaktiga, så behöver det inte alltid bero på att det är fel på mätningarna. Det kan istället vara de kända punkterna som har felaktiga lägen. Detta kan bero på att de har rört sig, att man har använt fel punkt eller att vi har angett fel koordinater. I utjämningen räknas alla kända punkter som perfekta och eventuella fel hos dem tolkas som mätningsfel istället. 

För att testa mätningarna utan påverkan från koordinatfel bör man därför genomföra en fri utjämning (alla punkter räknas som nya) för att få bort alla fel i mätningarna. Detta förutsätter att nätet i så stor utsträckning som möjligt hänger ihop i slingor – polygontåg mot anslutningspunkter ger ett osäkert resultat vid fri utjämning.

Om man fått bort alla mätfel i nätet så återstår att testa de kända punkternas lägen. Detta görs genom följande steg:

• Om man under Nätutj.|Inställningar|Generell valt Plan eller Plan och höjd så testas kända koordinater i plan. Om valet är Höjd så testas Z-koordinaterna istället.
• Testet startas genom att välja Tester|Kända punkter. Följande fönster dyker upp:

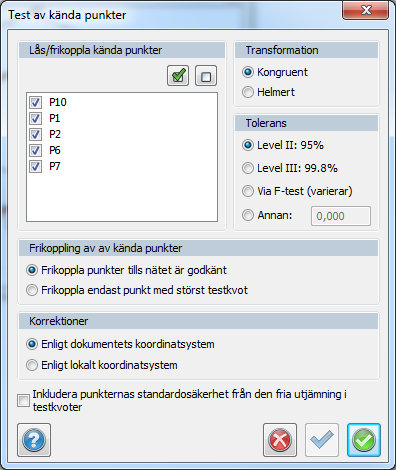
• Här väljer vi först vilka punkter som vi vill testa i listan Lås/frikoppla kända punkter. De punkter som är förbockade kommer att ingå i testet. Klickar vi på knappen Alla så kommer alla punkter att ingå. Knappen Ingen kopplar bort alla så att man sedan själv kan göra ett urval. På detta vis så har vi möjlighet att bara testa kända punkter i en viss del av nätet, vilket kan vara användbart i långsträckta nät.
• Programmet kan sedan ställas in för att stanna när en beräkning har skett (Frikoppla endast punkt med störst fel) eller frikoppla sämsta punkten och räkna om tills alla punkter klarar gränsvärdet (Frikoppla punkter tills nätet är godkänt). Det sistnämnda är snabbt och smidigt som ett första test, men den slutliga kontrollen bör helst göras punkt för punkt där man gör en noggrann analys innan man går vidare.
• När programmet beräknar längdmätningar så kan man ange under Korrektioner om längder ska korrigeras för Ellipsoid och Projektion. Om man väljer Enligt dokumentets koordinatsystem så gäller de korrektioner som är inställda generellt för projektet. Inställningarna kan kontrolleras under System/Projektinställningar|Koordinatsystem. Väljer man Enligt lokalt koordinatsystem så avaktiveras korrektionerna för Projektion och Ellipsoid. Observera att dessa val gäller oavsett vad man ställt in som snabbval under Nätutj.|Inställningar|Metod.

• Om Inkludera punkternas standardosäkerhet från den fria utjämningen i testkvoter är ikryssad så tas även punktosäkerheten från den fria utjämningen med när testkvoten beräknas. I HMKs beskrivning är denna ej med (ej ibockad ruta som default), men felteoretiskt borde osäkerheten i det fria nätet tas med i bedömningen, så det är upp till användaren att bestämma..

• Test av kända punkter har utvecklats för att följa metodbeskrivningar och krav i nya HMK2020, och har bl.a. med värden för att bedöma om en skalskillnad är signifikant utan att behöva använda externa transformationsfunktioner.

För att beskriva övriga inställningar så går vi igenom vad som händer om man startar testet genom att trycka på Beräkna:

• En fri utjämning genomförs. För de punkter som ska testas så plockas de koordinater ut som punkterna fick i den fria utjämningen. Dessa är felaktiga i och med att de kommer från en fri utjämning, men om denna är korrekt så ligger punkterna rätt relativt varandra.
• Programmet tar sedan testpunkternas koordinater från den fria utjämningen och transformerar dem för att passa in dem så bra som möjligt på de kända koordinaterna för samma punkter. 

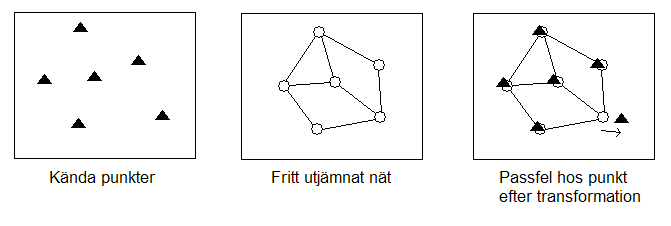
• Detta görs för test i plan genom förflyttning i X och Y, vridning och, om man valt det i programmet, skaländring. Detta val sker genom att välja Kongruent eller Helmert som Transformation. Den sistnämnda typen anpassar även det fria nätets skala, vilket gör att man tar bort påverkan av skalfel hos längdmätaren. Om man är säker på att längdernas skala är riktig så bör man använda Kongruent, som behåller längdernas skala. Det finns annars en liten risk att passfel hos punkter delvis tolkas som skalfel istället i beräkningen.
• I höjd sker transformationen genom att programmet beräknar medelvärden för både de kända och de utjämnade punkterna. Medelvärdet räknas sedan bort från kända respektive utjämnade koordinater så att bägges snitt blir noll (tyngdpunktsreducering).
• För höjder räknas det även ut medelfel för anslutningshöjdfixar även om de inte ingår i den fria utjämningen. Programmet letar då upp närmaste utjämnade höjd och använder medelfelets fortplantningslag på medelfelen för anslutningsmätningarna och den närmaste utjämnade punkten för att sätta ett medelfel för den höjdfix som man anslutit till. Detta värde har givetvis inte samma säkerhet som de höjdmedelfel som ingår i den fria utjämningen. Att utesluta dem skulle dock innebära att man inte fick med anslutnings-höjdfixarna alls i testet, vilket oftast är en större nackdel då denna mätsituation förekommer ganska ofta. 
• I plan testas endast de kända punkter som ingått i den fria utjämningen, dvs anslutningspunkter utesluts ur testet om inte mätningarna är överbestämda mot dem. Detta beror på att de är osäkra jämfört med det övriga nätet, då minst två okontrollerade mätningar (vinkel och längd) används. Det är dock vanligt i plan att anslutningsmätningarna är överbestämda så att punkterna ingår i det fria nätet. Vi har även situationer när bara en vinkel är mätt mot en känd punkt som är bakåtobjekt. Denna punkt blir i så fall omöjlig att testa och utesluts ur testet.
• Om de kända koordinaterna är korrekta (och även mätningarna i den fria utjämningen) så ska utjämnade och kända koordinater passa exakt på varandra vid en transformation. Om någon punkt är felaktig så märks det genom att den får ett passfel mellan fria och kända koordinater. Passfelet redovisas som fel uppdelat i X och Y samt radiellt (totalt) fel. Problemet är nu bara var man ska dra gränsen för när en punkt är felaktig, och i samband med detta ta hänsyn till de felkällor som finns i beräkningen. Dessa är främst punkternas medelfel från transformationen och den fria utjämningen. En punkt som ligger i utkanten av nätet blir t ex mer osäker i transformationen än en i mitten.
• För att få ett så säkert redskap som möjligt för att konstatera fel, så räknas en testkvot fram. Denna anger hur stort passfelet är jämfört med punktens sammanlagda medelfel från transformationen och den fria utjämningen i passfelets riktning. Detta testvärde kan jämföras med standardiserade förbättringar (sigmanivåer) för mätningar. Efter detta så kan HMK:s trenivåprincip tillämpas för att bedöma om en punkt är fel eller ej. Man kan ställa in i programmet om gränsen för fel ska dras vid faktorn 2 (95% sannolikhet för fel), 3 (99.8%), F-test (varierande gränsvärde) eller en egen nivå.

• När beräkningen är klar så redovisas hur många punkter som är låsta respektive frikopplade efter beräkningen. I rutan Aktuell punkt visas sämsta punktens ID och testkvot tillsammans med felet i X och Y, radiellt (totalt) och i vilken riktning (bäring) som punkten har rört sig. 

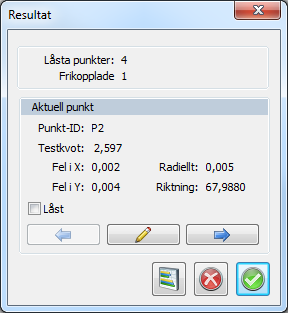
• Klickar man på Redigera så hoppar programmet till punktfliken och ställer sig på den aktuella punktens rad. Detta är till för att snabbt kunna kontrollera och eventuellt korrigera felaktiga koordinater för den aktuella punkten. Klickar man på Nästa så visas näst sämsta punkt och så vidare. Föreg. går sedan åt andra hållet.
• Vi kan också bocka för om punkten ska vara känd (Låst) eller frikopplad i nästa beräkning.
• För att få en sammanställning av en beräkning så klickar man på Rapport. Man väljer då vilken rapportmall som man vill använda (vanligtvis Standard) och får då upp en sammanställning av beräkningen. Rapporten visar först följande uppgifter:

• Sedan visas grundmedelfel, HMK:s godkäntgräns, överbestämningar och k-tal för den fria utjämning som ligger till grund för testet. Efter detta redovisas samma parametrar för en tvångsutjämning med alla punkter låsta och slutligen en tvångsutjämning med endast kvarvarande låsta punkter som kända. Tanken här är att man ska kunna se om de borttagna punkterna förbättrar nätet som helhet vid den sista utjämningen.
• Efter detta visas data för den/de punkter som kopplats bort. Följande data visas:

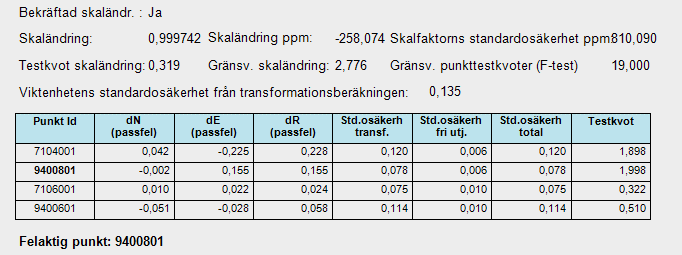
• Nästa del av rapporten är en redovisning av varje enskild sökning och dess resultat. Om vi har ställt in programmet på att bara göra en beräkning så visas den här. Har vi valt ”Frikoppla punkter tills nätet är godkänt” så redovisas alla separata beräkningar. Följande data ingår:

• Sedan visas för varje test följande tabell:

• Under tabellen visas slutsatsen:

• När man analyserat klart resultatet så kan man skriva ut eller spara resultatfilen i olika format m h a ikonerna längst uppe till vänster. För att återvända till testinställningarna så stänger man resultatfönstret och väljer OK, varpå man återvänder till testets första fönster. Om punkter har kopplats loss under eller efter senaste beräkningen så är de nu bortkopplade i listan Lås/frikoppla kända punkter. Vi kan nu välja att ändra inställningarna, koppla loss eller låsa punkter och beräkna igen. 
• När vi är färdiga med testet så trycker vi på Verkställ. Vi får då en fråga om vi vill att de punkter som kopplades loss i testet ska kopplas loss under punktfliken också. Då det kan vara känsligt att ge kända punkter nya koordinater bör man vara säker på följdverkningarna av detta. Faran är att man lätt får olika koordinater för en viss punkt i olika projekt, så de punkter som kopplas loss bör inte vara osäkra.

Nyckelord: Nätutjämning test av kända punkter, Test - test av kända punkter

Copyright © 2024 by Adtollo AB.

Created with the Personal Edition of HelpNDoc: Streamline Your Documentation Creation with a Help Authoring Tool